Vinn's Studio

Normalization & Standardization

Word count: 1.5kReading time: 6 min
2021/12/14 Share

特征工程中的一些常用特征缩放方法：归一化（Normalization）与标准化（standardization）。

Normalization & Standardization 的作用

特征缩放主要是为了：

  1. 消除量纲：使不同量纲的特征处于同一数量级，减少方差大/数量级大的特征的影响，使模型更准确；
  2. 加快学习算法的收敛速度；

Normalization & Standardization 的原理

假设一个数据集包括「身高」和「体重」两个特征（它们都满足正态分布），画出原始数据图像为：

Standardization

又叫 z-score 归一化。Standardization 能够将特征数据平移 + 缩放成一个均值为 0，方差为 1 的分布（不改变原始分布）： \[ x_i^{\prime}=\frac{x_i-\bar{x}_i}{\sigma_i} \] 其中：

  • \(x_i\) 表示某个样本的某个特征（\(i\)）的值；
  • \(x_i^{\prime}\) 表示经过变换后该样本的该特征的值；
  • \(\bar{x}_i\) 表示该特征的均值；\(\leftarrow\) 对所有样本的该特征值进行计算得到
  • \(\sigma_i\) 表示该特征的标准差；\(\leftarrow\) 对所有样本的该特征值进行计算得到

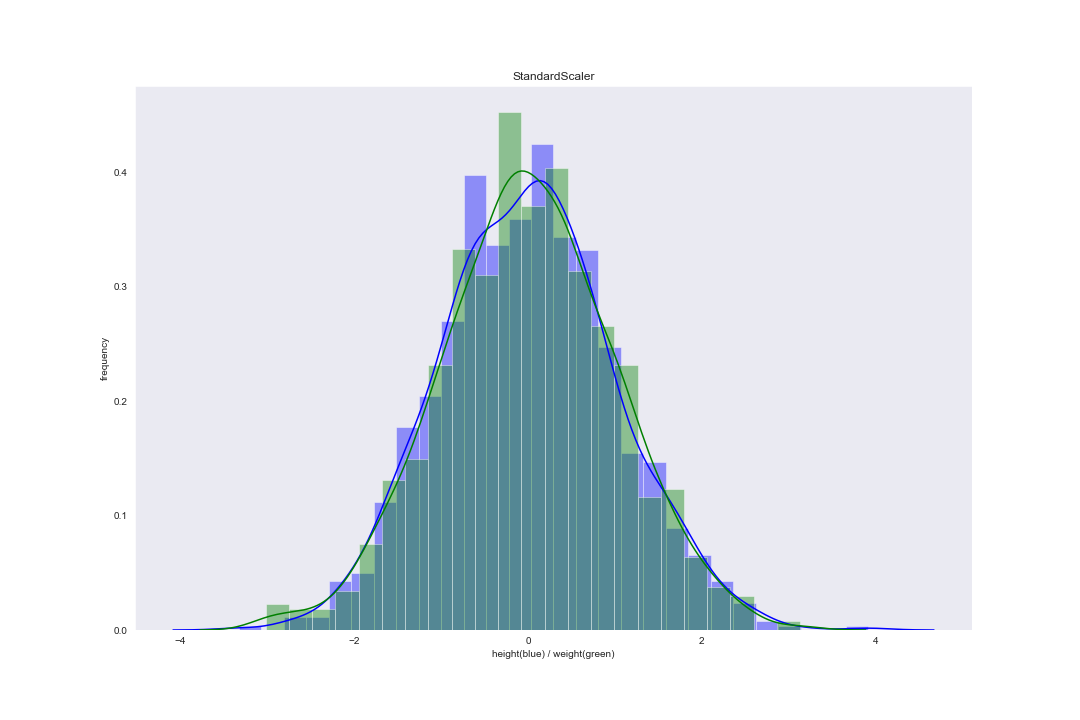
在 scikit-learn 库的 preprocessing 中，StandardScaler() 函数对应这一缩放方法。案例数据集使用 Standardization 后分布图像为：

Rescaling

又叫 min-max 归一化。Rescaling 将特征数据的取值范围平移 + 缩放到 0 和 1 之间（按比例缩放，不改变分布）： \[ x_i^{\prime}=\frac{x_i-\max(x_i)}{\max (x_i)-\min (x_i)} \] 其中：

  • \(x_i\) 表示某个样本的某个特征（\(i\)）的值；
  • \(x_i^{\prime}\) 表示经过变换后该样本的该特征的值；
  • \(\max(x_i)\) 表示该特征的最大值；\(\leftarrow\) 对所有样本的该特征值进行计算得到
  • \(\min(x_i)\) 表示该特征的最小值；\(\leftarrow\) 对所有样本的该特征值进行计算得到

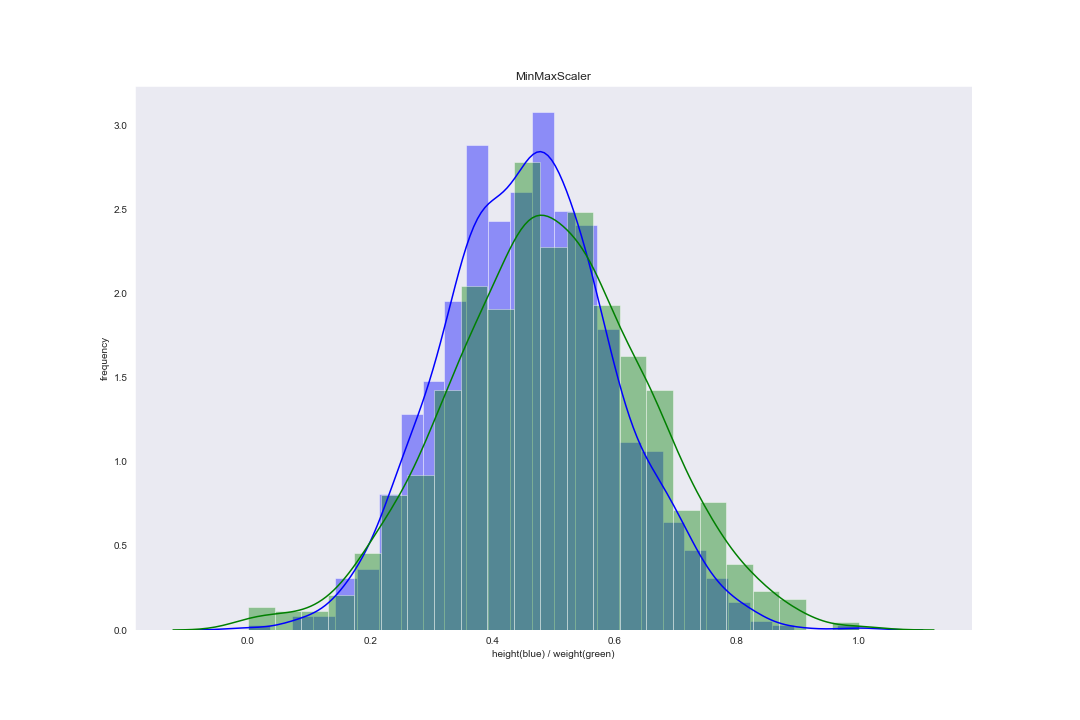
在 scikit-learn 库的 preprocessing 中，MinMaxScaler() 函数对应这一缩放方法。案例数据集使用 Rescaling 后分布图像为：

Mean Normalization

Mean Normalization 将特征数据平移为均值等于 0，缩放为取值范围区间长度为 1 的一个分布（按比例缩放，不改变分布）： \[ x_i^{\prime}=\frac{x_i-\bar{x}_i}{\max (x_i)-\min (x_i)} \] 其中：

  • \(x_i\) 表示某个样本的某个特征（\(i\)）的值；
  • \(x_i^{\prime}\) 表示经过变换后该样本的该特征的值；
  • \(\bar{x}_i\) 表示该特征的均值；\(\leftarrow\) 对所有样本的该特征值进行计算得到
  • \(\max(x_i)\) 表示该特征的最大值；\(\leftarrow\) 对所有样本的该特征值进行计算得到
  • \(\min(x_i)\) 表示该特征的最小值；\(\leftarrow\) 对所有样本的该特征值进行计算得到

Max Abs Scaler

Max Abs Scaler 将特征数据的取值范围缩放到 -1 和 1 之间（按比例缩放，不改变分布）： \[ x_i^\prime = \frac{x_i}{\max(|x_i|)} \] 其中：

  • \(x_i\) 表示某个样本的某个特征（\(i\)）的值；
  • \(x_i^{\prime}\) 表示经过变换后该样本的该特征的值；
  • \(\max(|x_i|)\) 表示该特征的最大绝对值；\(\leftarrow\) 对所有样本的该特征值进行计算得到

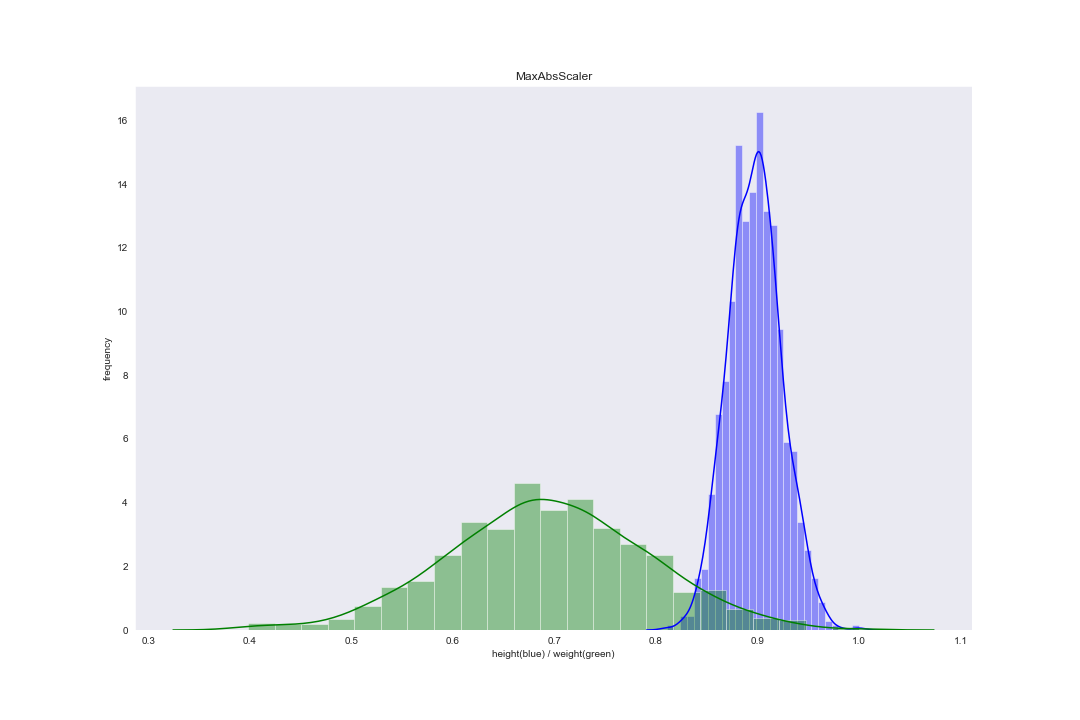
在 scikit-learn 库的 preprocessing 中，MaxAbsScaler() 函数对应这一缩放方法。案例数据集使用 Rescaling 后分布图像为：

Normalization

又叫 Scaling to unit length 归一化或 Length-one 归一化。该方法将每个样本的特征向量分别缩放为范数等于 1 的向量（保留原始数据的分布；由于样本特征向量范数被限定为 1，则特征数据的值域也被限定在 0 和 1 之间），从而剔除特征强度的影响： \[ x_i^{\prime}=\frac{x_i}{\|\vec{x}\|_p} \] 其中：

  • \(x_i\) 表示某个样本的某个特征（\(i\)）的值；
  • \(x_i^{\prime}\) 表示经过变换后该样本的该特征的值；
  • \(\|\vec{x}\|_p\) 表示该样本的特征向量 \(\vec{x}\) 的 p-范数（p-norm）的值；\(\leftarrow\) 对该样本的所有特征值进行计算得到

在 scikit-learn 库的 preprocessing 中，Normalizer() 函数对应这一缩放方法（默认为 L2-范数）。案例数据集使用 Rescaling 后分布图像为：

Robust Scaler

Robust Scaler 使用对异常值鲁棒的统计信息来缩放特征。使用该方法进行缩放可以减小异常值的影响： \[ x_{i}{ }^{\prime}=\frac{x_{i}-median(x_i)}{I Q R(x_i)} \] 其中：

  • \(x_i\) 表示某个样本的某个特征（\(i\)）的值；
  • \(x_i^{\prime}\) 表示经过变换后该样本的该特征的值；
  • \(median(x_i)\) 表示该特征的中位数；\(\leftarrow\) 对所有样本的该特征值进行计算得到
  • \(IQR(x_i)\) 表示该特征的四分位距（Inter-Quartile Range，即 25% 分位数和 75% 分位数之间的差值）；\(\leftarrow\) 对所有样本的该特征值进行计算得到

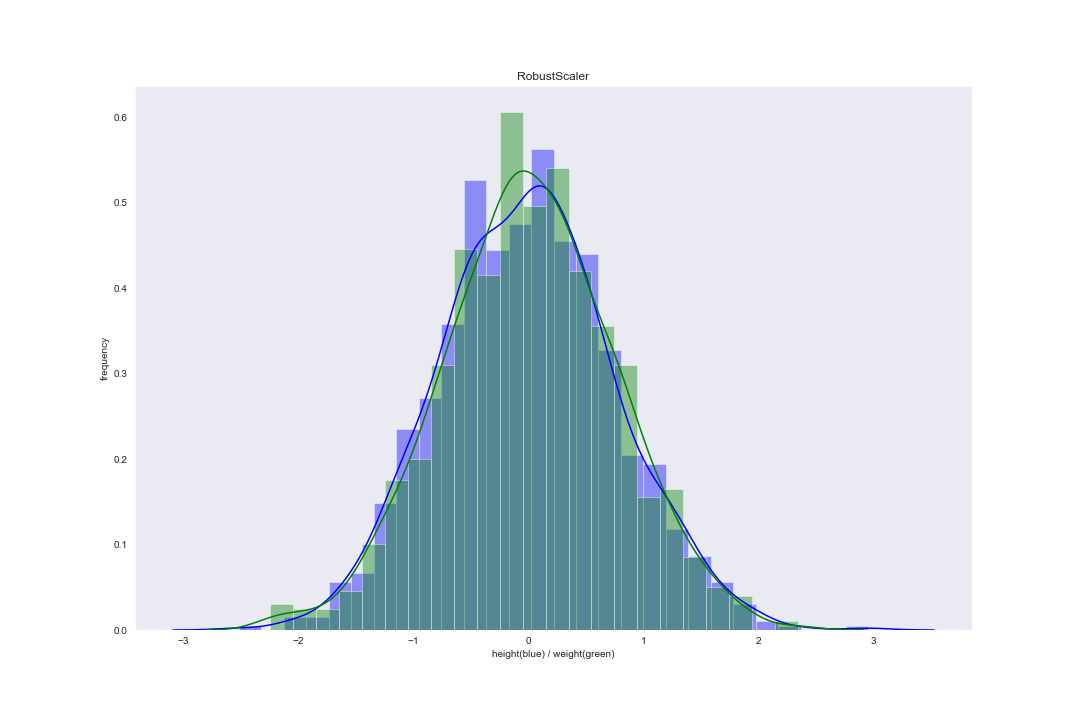
在 scikit-learn 库的 preprocessing 中，RobustScaler() 函数对应这一缩放方法（默认为 L2-范数）。案例数据集使用 Rescaling 后分布图像为：

Non-linear Normalization

非线性归一化对特征数据进行 log()、exp()、arctan()、sigmoid() 等非线性变换，以得到各种不同的效果：

  • log() 在 [0,1] 上有很强的区分度；
  • arctan() 可以将任意实数转换到 \([-\pi/2, \pi/2]\) 区间；
  • sigmoid() 可以将任意实数映射到 (0, 1) 区间；
  • 此外还有 Box-Cox 变换等更高级的变换方法；

Codes

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing

def plot(data, title):
    sns.set_style('dark')
    f, ax = plt.subplots(figsize=(15, 10))
    ax.set(ylabel='frequency')
    ax.set(xlabel='height(blue) / weight(green)')
    ax.set(title=title)
    sns.distplot(data[:, 0:1], color='blue')
    sns.distplot(data[:, 1:2], color='green')
    plt.savefig(title + '.png')
    plt.show()

# generate the data
np.random.seed(42)
height = np.random.normal(loc=168, scale=5, size=1000).reshape(-1, 1)
weight = np.random.normal(loc=70, scale=10, size=1000).reshape(-1, 1)

# plot the original data
original_data = np.concatenate((height, weight), axis=1)
plot(original_data, 'Original')

# standardization / z-score
standard_scaler_data = preprocessing.StandardScaler().fit_transform(original_data)
plot(standard_scaler_data, 'StandardScaler')

# rescaling / min max scaler
min_max_scaler_data = preprocessing.MinMaxScaler().fit_transform(original_data)
plot(min_max_scaler_data, 'MinMaxScaler')

# max abs scaler
max_abs_scaler_data = preprocessing.MaxAbsScaler().fit_transform(original_data)
plot(max_abs_scaler_data, 'MaxAbsScaler')

# normalization / Scaling to unit length
normalizer_data = preprocessing.Normalizer().fit_transform(original_data)
plot(normalizer_data, 'Normalizer')

# robust scaler
robust_scaler_data = preprocessing.RobustScaler().fit_transform(original_data)
plot(robust_scaler_data, 'RobustScaler')

Author：Lingfeng Zhu

Original Link：https://lingfengzhu.github.io/2021/12/14/Normalization-Standardization/

Published：December 14th 2021, 4:04:38 pm

Updated：February 8th 2022, 9:58:13 am

Copyright：This Article Uses Attribution-NonCommercial 4.0 International as the license

CATALOG
  1. Normalization & Standardization 的作用
  2. Normalization & Standardization 的原理
    1. Standardization
    2. Rescaling
    3. Mean Normalization
    4. Max Abs Scaler
    5. Normalization
    6. Robust Scaler
    7. Non-linear Normalization
  3. Codes
Total : 33
2022
2021
2020
NLP Survival Analysis COVID-19 Conda Docker Python Hexo Web-Frontend Pytorch RecSys
Deep-Learning Algorithm Statistics Syntax Machine-Learning Finance