DCN 全称 Deep & Cross Network,是谷歌和斯坦福大学在 2017 年提出的用于 Ad Click Prediction 的模型。
CTR 预估
CTR 预估的定义
CTR 全称为 Click Through Rate,指展示给用户的所有广告/商品中,被用户点击的广告/商品占的比例,即用户点击的概率。广告支付领域中一个非常流行的模型就是 CPC (cost-per-click),即按照用户的每次点击支付广告费。在这种付费方案下,准确地进行 CTR 预估,给用户推送他们最可能点击的广告/商品就非常重要了。
CTR 预估的发展
人们对 CTR 预估的建模大概经过如下几个阶段:
- 传统的 CTR 模型为了增强非线性表达能力,需要构造特征组合(手工特征工程),虽然这些特征含义明确、可解释性强,但通常需要大量的特征工程,耗时耗力;
- 之后出现的 FM (Factorization Machine) 使用隐向量的内积来建模组合特征;FFM 在此基础上引入 field 的概念,针对不同的 field 使用不同隐向量。这两者的都是针对低阶的特征组合进行建模的,且隐变量不具备可解释性;
- 随着 DNN 在计算机视觉、自然语言处理、语音识别等领域取得重要进展,其几乎无限的表达能力被广泛的研究,同样也被用来解决 CTR 预估问题中输入特征高维高稀疏的问题。DNN 可以对高维组合特征进行建模,引入DNN之后,依靠神经网络强大的学习能力,可以一定程度上实现自动获取高阶的非线性特征组合,然而这些特征通常也是隐式的,含义难以解释;
- Wide & Deep Network (WDL,Wide & Deep Learning) 模型融合了手工特征工程和深度学习模型的特点,将 wide 侧手工构造(hand-craft)的特征组合与 deep 侧 DNN 生成的特征组合拼接起来进行训练,兼具了特征工程的可解释性以及深度学习模型的强大泛化性能;
- WDL 中 Wide 侧的交叉组合特征依然需要依靠 hand-craft 来完成。在 WDL 基础上提出的 DCN 能对 sparse 和 dense 的输入自动学习特征交叉组合,可以有效地捕获有限阶(bounded degrees)的有效特征组合,无需人工(hand-craft)特征工程或暴力搜索(exhaustive searching),并且计算代价较低。
特征组合/特征交叉 (Feature Crosses):为了提高复杂关系的拟合能力,在特征工程上经常会把普通特征(称为一阶特征)以某种结构相互组合,构成高阶组合特征/交叉特征。例如,将两个特征的值相乘、对某个特征做平方等,都能得到组合特征/交叉特征。
特征的阶(degree):可以类比多项式的阶,两个普通特征相乘得到的组合特征称为二阶特征,三个普通特征相乘得到的组合则称为三阶特征,一个特征的平方也是二阶特征,一个特征的立方则是三阶特征,以此类推。决策树中每条从根到叶的路径都可以视为一个高阶组合特征(该路径上涉及到的普通特征越多,则该组合特征阶数越高)、神经网络的每个神经元其实也都可以视作一个高阶组合特征(该神经元的计算涉及到的普通特征越多,则该组合特征阶数越高)。
Deep & Cross Network
DCN 全称 Deep & Cross Network,是谷歌和斯坦福大学在 2017 年提出的用于 Ad Click Prediction 的模型。DCN 在学习特定阶数组合特征的时候效率非常高,而且同样不需要特征工程,引入的额外的复杂度也是微乎其微的。
DCN 的特点/优势
- 在 WDL 的结构基础上,提出一种新型的交叉网络结构(Cross Network)替代 Wide 侧的 hand-craft 特征:Cross Network 在每一层都应用 feature crossing,高效地学习了有限阶数 (bounded degree) 的组合特征,不需要人工设计的特征工程;
- Cross Network 网络结构简单且高效:可以获得多项式阶(polynomial degree)交叉特征,且阶数随网络层数(layer depth)的增加而增加;
- 与 DNN 模型相比,DCN 具有较少的参数规模(参数的数量将近少了一个数量级),却取得了较好的效果(DCN 的 logloss 更低),更易于使用;
- 与 FM 模型相比,DCN 同样基于参数共享机制(参数共享不仅使得模型更加高效,还能使得模型可以泛化到之前没有出现过的特征组合,并且对噪声的抵抗性更加强),但是 FM 是一个非常浅的结构,并且限制在表达二阶组合特征上,DCN 则把这种参数共享的思想从一层扩展到多层,并且可以学习高阶的特征组合。FM 的高阶版本的变体也能学习高阶特征,与它们相比,DCN 的优势在于:其参数规模随着输入维度的增长是线性增长的趋势。
DCN 的网络结构
DCN 的架构与 WDL 非常类似:
- 底层为 Embedding and stacking layer:对输入特征进行初步处理;
- 中间层为并行的 Cross Network 以及 Deep Network:两部分同步进行;
- 输出层为 Combination output Layer:将两部分 network 的结果拼接并处理成最终输出;
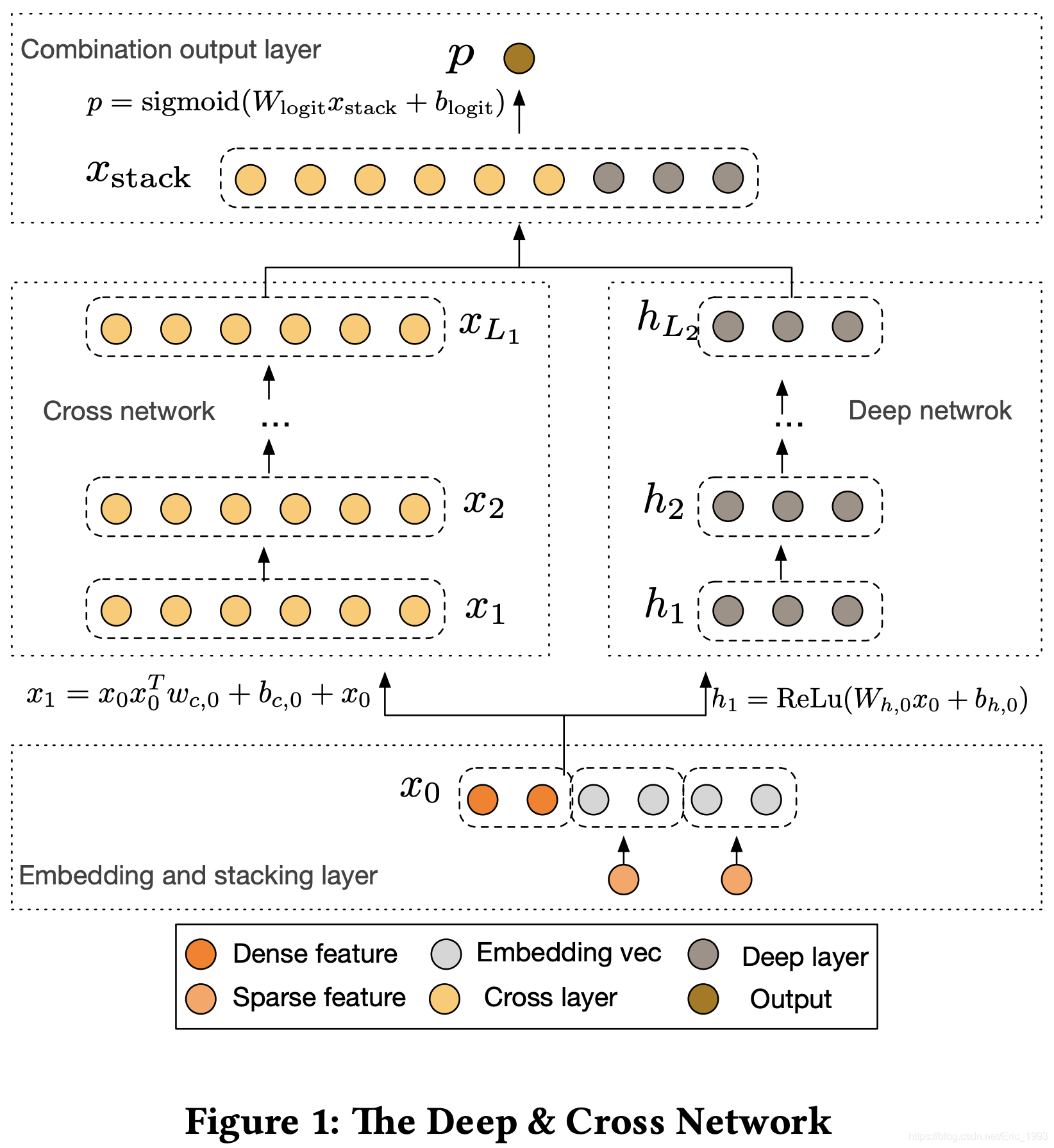
DCN 的原理
Embedding and Stacking Layer
Embedding
原始的输入特征一般包括离散的类别特征 (Categorical Features) 和连续的稠密特征 (Dense Features)。通常会将类别型特征编码为 OneHot 的形式再输入模型。但是,对于类别数较多的特征,其 OneHot 编码的维度较高且通常较为稀疏(高维且稀疏的特征空间),不利于后续模型处理。因此,针对这部分类别型特征,引入一个 Embedding 层将它们的 OneHot 编码映射为低维的稠密特征(dense vectors with real values): \[ \vec{x}_{e m b, i}=W_{e m b, i} \vec{x}_{i} \] 其中:
- \(\vec{x}_i \in \mathbb{R}^{n_i}\) 是样本的第 \(i\) 个需要嵌入的类别型特征的 OneHot 编码向量,\(n_i\) 表示该类别型特征的类别数;
- \(\vec{x}_{e m b, i} \in \mathbb{R}^{n_e}\) 是 对该类别型特征进行 embedding 的结果,\(n_e\) 为 embedding 后的嵌入向量的维度(作为一个超参数需要开发者自行设定);
- \(W_{e m b, i} \in \mathbb{R}^{n_e \times n_i}\) 是该类别型特征对应的 embedding matrix,负责将 \(\vec{x}_i\) 映射为 \(\vec{x}_{emb,i}\),它会与网络中的其它参数一起被训练。
Stacking
将上述经过 embedding 处理的类别特征嵌入向量 \(\vec{x}_{emb,i}, i\in\{1,2,3,...,k\}\) (其中 \(k\) 表示需要嵌入的类别型特征的总个数)与经过归一化 (normalization) 的所有连续型特征(以及不需要进行嵌入操作的那些类别型特征的 OneHot 编码) \(\vec{x}_{dense}\) 拼接 (concatenation) 在一起,输入后续步骤的网络中: \[
\vec{x}_{0}=\left[\vec{x}_{e m b, 1}^{T}, \vec{x}_{e m b, 2}^{T}, \ldots, \vec{x}_{e m b, k}^{T}, \vec{x}_{\text {dense }}^{T}\right]^{T}
\] 在 TensorFlow 中,这部分可以通过 tf.feature_column 提供的 API 实现:
1 | # 特征 |
Cross Network
交叉网络的核心思想是显式并且高效地对交叉特征进行学习。交叉网络由多个交叉层 (Crossing Layer) 组成,每个交叉层具有以下前向传播公式: \[ \vec{x}_{l+1}=\vec{x}_{0} \vec{x}_{l}^{T} \vec{w}_{l}+\vec{b}_{l}+\vec{x}_{l}=f\left(\vec{x}_{l}, \vec{w}_{l}, \vec{b}_{l}\right)+\vec{x}_{l} \] 其中:(\(d\) 为输入 Cross Network 的特征向量的维度)
- \(\vec{x}_{l}, \vec{x}_{l+1} \in \mathbb{R}^{d}\) 分别表示第 \(l\) 层和第 \(l+1\) 层的输出向量;
- \(\vec{w}_{l}, \vec{b}_{l} \in \mathbb{R}^{d}\) 分别表示第 \(l\) 层的权重与偏置;\(\leftarrow\) 即第 \(l\) 层与第 \(l+1\) 层之间的连接参数
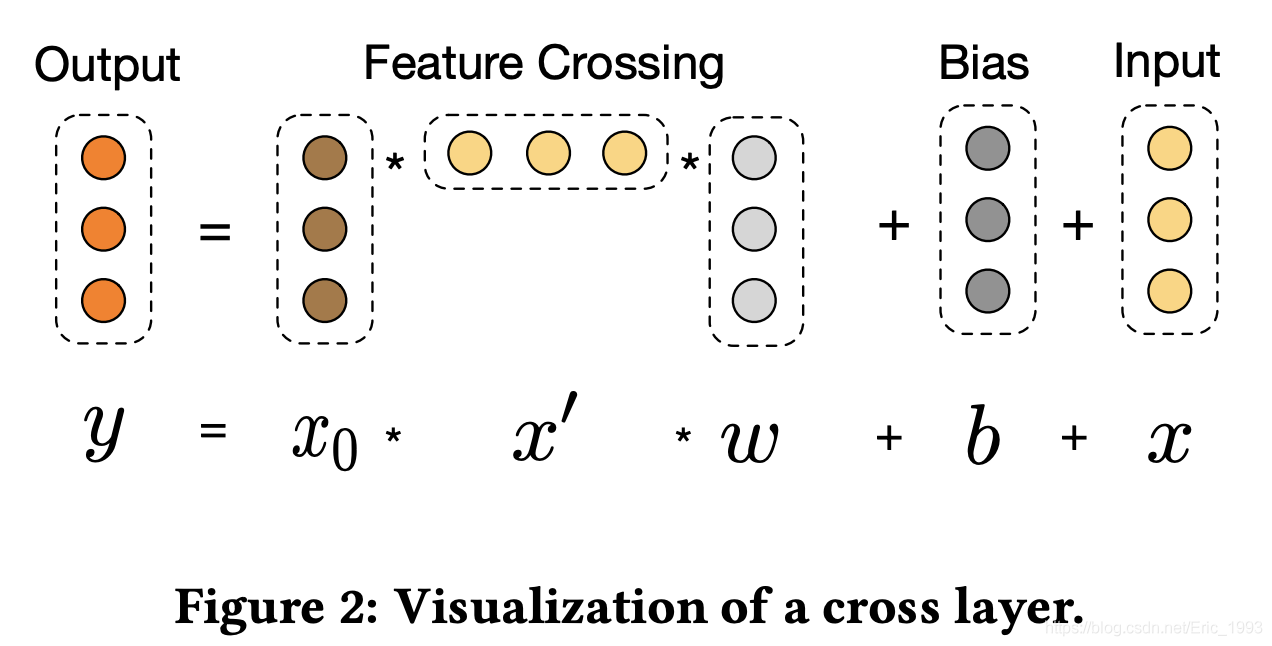
残差网络 (Residual Network) 的思想:若定义 \(f\left(\vec{x}_{l}, \vec{w}_{l}, \vec{b}_{l}\right) = \vec{x}_{0} \vec{x}_{l}^{T} \vec{w}_{l}+\vec{b}_{l}\),则每一层的公式可以写作 \(\vec{x}_{l+1}=f\left(\vec{x}_{l}, \vec{w}_{l}, \vec{b}_{l}\right)+\vec{x}_{l}\),即每一层的输出 = 上一层拟合的交叉特征 \(f\) + 上一层的输出(即当前层的输入)。不难看出,此处拟合交叉特征的 mapping function \(f: \mathbb{R}^d \rightarrow \mathbb{R}^d\) 恰好满足 \(f = \vec{x}_{l+1} - \vec{x}_l\) ,可以视作 \(f\) 拟合了第 \(l+1\) 层的残差(该层的输出 - 该层的输入) ,这里的设计借鉴了残差网络的思想。
高阶交叉特征 (high-degree interaction/across feature):cross network 的独特结构使得交叉特征的阶数 (the degress of cross features) 随着 cross layer 的深度增加而增长。以 \(\vec{x}_0\) 为基准(即将其视为普通一阶特征),有:
- 第 1 层 layer 输出的 \(\vec{x}_1\) 中关于 \(\vec{x}_0\) 的最高阶多项式为 \(\vec{x}_0 \vec{x}_0^T\vec{w}_0\),它关于 \(\vec{x}_0\) 的阶为 2;
- 第 2 层 layer 输出的 \(\vec{x}_2\) 中关于 \(\vec{x}_0\) 的最高阶多项式为 \(\vec{x}_0 (\vec{x}_0 \vec{x}_0^T\vec{w}_0)^T\vec{w}_1\),它关于 \(\vec{x}_0\) 的阶为 3;
- ...
- 第 \(l\) 层 layer 输出的 \(\vec{x}_{l+1}\) 中关于 \(\vec{x}_0\) 的最高阶多项式关于 \(\vec{x}_0\) 的阶为 \(l+1\);
显然,交叉特征的阶数随着 cross layer 的深度增加而线性增长。
复杂度分析:假设 \(L_c\) 表示 cross layers 的层数, \(d\) 表示输入向量 \(\vec{x}_0\) 的维度。则在 cross network 中涉及的参数量为:\(L_c \times d \times 2\) (共有 \(L_c\) 层,每层有 2 个需要训练的参数向量 \(\vec{w}\) 与 \(\vec{b}\),每个参数向量维度为 \(d\))。
Cross Network 部分的时间和空间复杂度相对于输入向量的维度 \(d\) 是线性关系。因此,比起 DCN 的 Deep 部分,Cross Network 部分引入的复杂度微不足道,DCN 的整体复杂度与 Deep 部分的传统 DNN 在同一水平线上。如此高效 (efficiency) 是受益于公式中 \(\vec{x}_{0} \vec{x}_{l}^{T}\) 结构(两个向量的叉乘/外积)的 rank-one 特性:该结构的秩为 1,它可以使我们无需计算或存储整个 matrix 就生成所有的交叉项 (Cross terms)。
在代码实现 Cross Network 部分时,计算 \(\vec{x}_{0} \vec{x}_{l}^{T} \vec{w}_{l}\) 有两种计算顺序:(附 TensorFlow 实现)
先计算 \(\vec{x}_{0} \vec{x}_{l}^{T}\):该方法非常消耗计算和存储资源。显式地计算 \(\vec{x}_{0} \vec{x}_{l}^{T}\) 会得到一个 \(d \times d\) 的矩阵,需要非常大的内存空间来存储临时计算结果,且该矩阵继续与 \(\vec{w}_{l}\) 相乘也会消耗大量计算资源;
即使你在离线训练时通过减少 cross layer 的个数、减小 batch_size 等手段完成了模型的训练,在模型部署上线之后,线上的打分系统依然要面临 Out of Memory 的风险,因为线上预测时我们总是希望一次请求尽可能返回多条记录的预测分数,否则要么是影响全局的效果,要么是需要更多的请求次数,从而面临巨大的性能压力。
1
2
3
4
5
6
7
8
9def cross_layer(x0, x, name):
with tf.variable_scope(name):
input_dim = x0.get_shape().as_list()[1]
w = tf.get_variable("weight", [input_dim], initializer=tf.truncated_normal_initializer(stddev=0.01))
b = tf.get_variable("bias", [input_dim], initializer=tf.truncated_normal_initializer(stddev=0.01))
xx0 = tf.expand_dims(x0, -1) # shape <?, d, 1>
xx = tf.expand_dims(x, -1) # shape <?, d, 1>
mat = tf.matmul(xx0, xx, transpose_b=True) # shape <?, d, d>
return tf.tensordot(mat, w, 1) + b + x # shape <?, d>先计算 \(\vec{x}_{l}^{T} \vec{w}_{l}\):由于矩阵乘法服从结合律,因此也可以使用这种计算顺序。计算 \(\vec{x}_{l}^{T} \vec{w}_{l}\) 得到的结果是一个标量,几乎不占用存储空间,且该标量继续与 \(\vec{x}_{0}\) 相乘需要的计算资源也不大;
1
2
3
4
5
6
7def cross_layer2(x0, x, name):
with tf.variable_scope(name):
input_dim = x0.get_shape().as_list()[1]
w = tf.get_variable("weight", [input_dim], initializer=tf.truncated_normal_initializer(stddev=0.01))
b = tf.get_variable("bias", [input_dim], initializer=tf.truncated_normal_initializer(stddev=0.01))
xb = tf.tensordot(tf.reshape(x, [-1, 1, input_dim]), w, 1) # 对于向量,使用 tf.reshape 可以直接实现转置
return x0 * xb + b + x
显然,应该选择第二种计算顺序。
构建整个交叉网络的 TensorFlow代码如下:
1 | def build_cross_layers(x0, params): |
正是因为 Cross network 的参数比较少,导致它的表达能力受限,为了能够学习高度非线性的组合特征,DCN 并行地使用了 Deep Network 部分。
对于 Cross layer 可以换一种理解方式:
假设 \(\vec{x}_l \in \mathbb{R}^{d}\) 是一个 Cross layer 第 \(l+1\) 层的输入。首先构建 \(d^2\) 个 pairwise 的交叉项 \(x_{0,i}x_{l,j}\)(其中 \(x_{0,i}\) 表示 \(\vec{x}_0\) 的第 \(i\) 个分量;\(\tilde{x}_j\) 表示 \(\vec{x}_l\) 的第 \(j\) 个分量),将他们排列为长为 \(d^2\) 的列向量。然后基于 \(\vec{w}_l\) 构建一种内存高效的方式将它们投影为 \(d\) 维向量。如果采用全连接 Layer 那样直接投影的方式会带来 \(d^3\) 的开销,而 Cross layer 提供的投影方式仅需 \(d\) 的开销: \[ (\vec{x}_{0} \vec{x}_l^{T} \vec{w}_{l})^{T}=\left[\begin{array}{lll} x_{0,1}x_{l,1} \ldots x_{0,1}x_{l,d} & \ldots & x_{0,d}x_{l,1} \ldots x_{0,d}x_{l,d} \end{array}\right] \left[\begin{array}{cccc} \mid & & & \\ \vec{w}_l & 0 & \ldots & 0 \\ \mid & & & \\ & \mid & & \\ 0 & \vec{w}_l & \ldots & 0 \\ & \mid & & \\ \vdots & \vdots & \ddots & \vdots \\ & & & \mid \\ 0 & 0 & \ldots & \vec{w}_l \\ & & & \mid \end{array}\right] \] 上式中的矩阵即算法构建的投影矩阵。该矩阵具有一个块对角化结构,其中 \(\vec{w}_l \in \mathbb{R}^d\) 为权重列向量。
Deep Network
交叉网络的参数数目少,从而限制了模型的能力 (capacity)。为了捕获高阶非线性交叉特征,DCN 平行引入了一个深度网络 (Deep Network)。深度网络就是一个普通的全连接前馈神经网络,每个深度层具有如下公式: \[ h_{l+1}=f\left(W_{l} h_{l}+b_{l}\right) \] 其中:
- \(h_{l} \in \mathbb{R}^{n_{l}}, h_{l+1} \in \mathbb{R}^{n_{l+1}}\) 分别表示第 \(l\) 层与第 \(l+1\) 层的输出;
- \(n_l, n_{l+1}\) 分别表示第 \(l\) 层与第 \(l+1\) 层的神经元个数;
- \(W_{l} \in \mathbb{R}^{n_{l+1} \times n_{l}}, b_{l} \in \mathbb{R}^{n_{l+1}}\) 为第 \(l\) 层的权重与偏置;\(\leftarrow\) 即第 \(l\) 层与第 \(l+1\) 层之间的连接参数
- \(f(\cdot)\) 为激活函数,此处为 ReLU
可以为网络加入 Dropout、BatchNorm 之类的技术,但作者在论文 4.2 节的实现细节中说没有发现 Dropout 或者 L2 正则化有效。
复杂度分析:出于简洁性考虑,假设所有 Deep Layer (包括 Hidden Layers 以及 Output Layer) 的神经元个数均为 \(m\),共有 \(L_d\) 层 Deep Layers,输入向量 \(\vec{x}_0\) 的维度为 \(d\),则在 deep network 中涉及的参数量为: \[ (d + 1) \times m + (m^2 + m) \times (L_d - 1) \] 其中,输入层与第一个隐藏层之间的权重矩阵为一个 \(d \times m\) 矩阵,偏置为一个 \(m\) 维向量,故此处有 \((d+1)\times m\) 个参数;Deep Layers 之间的权重矩阵为 \(m\times m\) 矩阵,偏置为 \(m\) 维向量,\(L_d\) 个层间共有 \(L_d - 1\) 处间隙,因此这部分的参数量为 \((m^2 + m) \times (L_d - 1)\)。
构建深度网络的 TenorFlow 代码如下:
1 | def build_deep_layers(x0, params): |
Combination Layer
最后,将两个 Network 的输出进行拼接 (concatenate),然后将该拼接向量 (concatenated vector) 喂给一个标准的逻辑回归 (Logistic Regression) 模型: \[ p=\sigma\left(\left[x_{L_{c}}^{T}, h_{L_{d}}^{T}\right] w_{\text {logits }}\right), \quad \sigma(x)=\frac{1}{1+e^{-x}} \] 这一步的损失函数为带有 L2 正则项的标准 LR 模型的损失函数 (Negative Log Likelihood) : \[ \operatorname{loss}=-\frac{1}{N} \sum_{i=1}^{N} y_{i} \log \left(p_{i}\right)+\left(1-y_{i}\right) \log \left(1-p_{i}\right)+\lambda \sum_{l}\left\|\boldsymbol{w}_{l}\right\|^{2} \] 类似于 WDL 模型,训练过程中对两个并行部分进行 jointly train,且在训练期间,每个独立的 Network 可以察觉到另一个的存在。下面给出的是整个模型的完整 TensorFlow 实现代码:
1 | def dcn_model_fn(features, labels, mode, params): |
代码实现
TensorFlow 的部分代码实现已插附在原理部分,下面是 DeepCTR-Torch 对 CrossNet 部分的 PyTorch 实现:
1 | class CrossNet(nn.Module): |
在 __init__() 方法中初始化一个 Cross Network 层:
- 其中
layer_num表示 Cross Network 的层数; - 由于此处 Weight 和 Bias 均为向量,代码中使用 PyTorch 中的 Parameter 来表示,每一层 Weight/Bias 的 shape 为
[in_features, 1](in_features表示每个样本的维度, 即输入特征的维度);
在 forward 方法中实现 Cross Network 的前向传播逻辑:
- 其中
inputs的 shape 为[Batch_size, in_features]; x_0 = inputs.unsqueeze(2)对inputs的维度数量进行拓展,在dim = 0和dim = 1的基础上新增一个维度dim=2,此时inputs的 shape 被扩充为[Batch_size, in_features, 1];xl_w = torch.tensordot(x_l, self.kernels[i], dims=([1], [0]))计算了 \(\vec{x}_{l}^{T} \vec{w}_{l}\) 部分,此处torch.tensordot()将当前的x_l与第 \(i\) 层的 Weightkernels[i]进行点乘/内积,具体计算方法为:按照x_l(shape 为[Batch_size, in_features, 1]) 的dim=1维度(即in_features)与kernel[i](shape 为[in_features, 1]) 的dim=0维度(即in_features)进行 element-wise 逐元素相乘并求和,最后得到的xl_w即为 \(\vec{x}_{l}^{T} \vec{w}_{l}\) (此处 \(l = i\)),它的 shape 为[Batch_size, 1, 1];dot_ = torch.matmul(x_0, xl_w)则将 \(\vec{x}_{0}\) (shape 为[Batch_size, in_features, 1])与 \(\vec{x}_{l}^{T} \vec{w}_{l}\)(shape 为[Batch_size, 1, 1])相乘,计算得到的dot_即为 \(\vec{x}_{0} \vec{x}_{l}^{T} \vec{w}_{l}\)。dot_的 shape 为[Batch_size, in_features, 1];x_l = dot_ + self.bias[i] + x_l步骤将 Cross Network 第 \(i\) 层前向传播公式的各个部分相加(其中bias[i]的 shape 从[in_features, 1]被 boardcast 为[Batch_size, in_features, 1]);x_l = torch.squeeze(x_l, dim=2)对x_l的维度数量进行缩减,将dim=2维度取消,x_l的 shape 从[Batch_size, in_features, 1]被缩减为[Batch_size, in_features];