Vinn's Studio

Trie Tree

Word count: 5.1kReading time: 20 min
2021/01/06 Share

字典树 (Trie Tree) 经常被用于搜索引擎系统。下面是一些最基本的介绍。

1. 基本介绍

1.1. 定义

字典树，又称单词查找树或前缀树（Prefix Tree），是一种树形结构，是一种哈希树的变种。 ### 1.2. 应用 典型应用是用于统计、排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计，或是用于通讯录储存等。 ### 1.3. 结构 1. 根节点不包含字符，便于插入和查找； 2. 字典树的每条边都可以表示一个字母（代码实现中：用“某节点的值 value”表示“该节点指向它父节点的边”对应的字母）； 3. 字典树的每个节点有一个 bool 属性 isEnd：用于标记该节点是否是某个序列的终止节点； 4. 从根节点到任意一个终结节点，所经过的边上的所有字母表示一个单词； 5. 有相同前缀的单词共用前缀节点； 6. 每个节点的所有“直接连接的子节点”包含的字符都不相同：例如，在单词只包含小写字母和空格的情况下，每个节点最多有 26+1 个“直接连接的子节点”； 7. 字典树的每个节点可以有一个 int 属性 count：用于统计在插入的所有序列中，此节点被使用到的次数（在删除序列时，可以用到这个参数判断是否可以删掉这个节点）； 8. 字典树的每个节点可以有一个指向其父节点的指针 parent：如果需要找到某个节点的前缀序列时，可以用到这个指针；

例如，下图就是由单词 cat, her, him, no, nova 组成的一颗字典树。

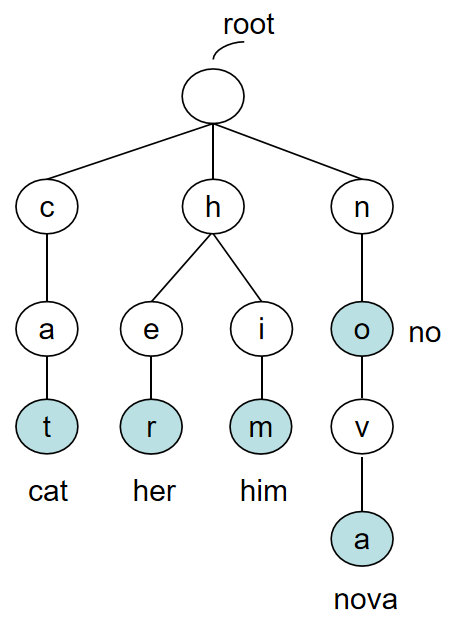
1.4. 优缺点

Trie Tree 的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的 * 优点：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。相比于哈希树，字典树还有以下优势： 1. 可以找到具有同一前缀的全部键值； 2. 可以按照词典序枚举字符串的数据集； 3. 随着哈希表大小的增加，会出现大量的哈希冲突，时间复杂度可能增加到 \(O(n)\)，其中 n 是插入的键的数量；与哈希表相比，Trie 树在存储多个具有相同前缀的键时可以使用较少的空间，此外 Trie 树只需要 \(O(m)\) 的时间复杂度，其中 m 为键长，而在平衡树中查找键值需要 \(O(mlogn)\) 时间复杂度。 * 缺点：Trie 树的内存消耗非常大：如果对于每个节点都要开辟 26 个子节点，则会消耗大量空间。（当然，或许用左儿子右兄弟的方法建树的话，可能会好点）

2. 代码实现

首先创建 TrieNode 类和 Trie 类。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 定义字典树的节点
class TrieNode(object):
    def __init__(self, value=None, count=0, parent=None):
        # 值：记录此节点对应的字符
        self.value = value
        # 频数统计：统计在插入的所有序列中，此节点被使用到的次数
        self.count = count
        # 父结点：记录此节点的父节点
        self.parent = parent
        # 子节点：记录此节点的所有子节点：以 {value: TrieNode} 的形式
        self.children = {}
        # 终止符号：标记此节点是不是终止节点
        self.isEnd = False

# 定义字典树
class Trie(object):
    def __init__(self):
        # 创建空的根节点
        self.root = TrieNode()

2.1. 插入操作：将一个序列插入字典树

从左到右扫这个序列，从根节点开始： * 如果当前字母在当前节点的子节点中没有出现过，就将该字母插入到当前节点的子节点中，并将插入的这个节点作为当前节点继续插入下一个字母； * 如果当前字母在当前节点的子节点中出现，则沿着字典树往下走到对应的子节点，且该节点的 count 属性加一，然后继续比较下一个字母； 最后当整个序列插入完毕时，将序列最后一个节点的 isEnd 属性设置为 True 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 插入操作
def insert(self, sequence):
    """
    基操，插入一个序列
    :param sequence: list, 需要插入的序列
    :return:
    """
    cur_node = self.root
    for item in sequence:
        if item not in cur_node.children:
            # 插入结点
            child = TrieNode(value=item, count=1, parent=cur_node)
            cur_node.children[item] = child
            # 将插入的节点作为新的当前节点
            cur_node = child
        else:
            # 沿着字典树往下走到对应的子节点
            cur_node = cur_node.children[item]
            cur_node.count += 1
    # 最后标记终止节点
    cur_node.isEnd = True

2.2. 查找操作：查询一个序列是否在字典树中

从左往右以此扫描这个序列，从根节点开始： * 如果当前字母在当前节点的子节点中没有出现过，则结束查找，字典树中没有这个序列； * 如果当前字母在当前节点的子节点中出现，则沿着字典树往下走到对应的子节点，然后继续比较下一个字母； 当走到序列的最后一个字母时，考虑对应节点的 isEnd 属性： * 如果最后一个字母对应的节点是终止节点，则说明目标序列是字典树中的一个完整序列； * 如果最后一个字母对应的节点不是终止节点，则说明目标序列只是字典树中一些序列的前缀部分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 查询操作
def search(self, sequence):
    """
    基操，查询是否存在完整序列
    :param sequence: list, 需要查询的序列
    :return mask: bool, 表示在字典树中是否查到该序列
    """
    cur_node = self.root
    mark = True # 用于标记是否查询到目标序列
    for item in sequence:
        if item not in cur_node.children:
            mark = False
            break
        else:
            cur_node = cur_node.children[item]
    # 如果目标序列的最后一个节点不是终止节点，则说明目标序列只是字典树中某些序列的前缀部分
    if not cur_node.isEnd:
        mark = False
    return mark

2.3. 删除操作：从字典树中删去一个序列

从左往右以此扫描这个序列，从根节点开始，只要目标序列存在于树中，则当前字母一定在在当前节点的子节点中，将当前字母对应的节点的频数计数减去 1： * 若频数减少到 0：表明剩下所有序列都不再需要该节点，因此删去该节点及其所有后代； * 否则：则沿着字典树往下走到对应的子节点，然后继续比较下一个字母； 最后，如果没有节点被实际删去，说明目标序列只是字典树中某些序列的前缀，删除操作只是将相关节点的频数计数减少了 1，因此，需要将目标序列最后一个节点的 isEnd 值重新设置为 False 表示该序列被删除了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 删除操作
def delete(self, sequence):
    """
    基操，删除序列，准确来说是减少计数
    :param sequence: list, 需要删除的序列
    :return mark: bool, 表示该序列是否在字典树中
    """
    mark = False # 用于标记是否查询到目标序列
    isDeleted = False # 用于标记是否有节点被实际删去
    if self.search(sequence):
        mark = True
        cur_node = self.root
        for item in sequence:
            # 目标序列涉及到的节点的频数计数 -1
            cur_node.children[item].count -= 1
            # 若目标序列涉及到的某个节点的频数计数减少到 0 时，删去该节点；
            # 被删去的节点的所有后代节点都随着该节点一起被直接删去了，因此可以直接 break；
            # 注意：目标序列的最后一个节点肯定也被同时删去了，因此不需要对任何节点的 isEnd 进行操作
            if cur_node.children[item].count == 0:
                cur_node.children.pop(item)
                isDeleted = True # 有节点被实际删去了
                break
            # 否则继续进入下一个节点
            else:
                cur_node = cur_node.children[item]
        # 如果没有节点被实际删去，说明目标序列只是字典树中某些序列的前缀，删除操作只是将相关节点的频数计数减少了 1
        # 因此，需要将目标序列最后一个节点的 isEnd 值重新设置为 False 表示该序列被删除了
        if not isDeleted:
            cur_node.isEnd = False
    return mark

2.4. 进阶：查找序列片段在字典树中的所有前缀或后缀

递归的思路：对于字典树中所有能与目标序列片段完全匹配的部分，分别记录下它们的前缀和后缀并汇总即可。具体思路见代码。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
# 进阶：查找序列片段在字典树中的所有前缀或后缀
def search_part(self, sequence, prefix, suffix, start_node=None):
    """
    递归查找子序列，返回前缀和后缀结点
    此处简化操作，仅返回一位前后缀的内容与频数
    :param sequence: list, 输入的序列片段
    :param prefix: dict, {value:count}, 用于保存得到的所有前缀及其对应的频数，初始传入空字典
    :param suffix: dict, {value:count}, 用于保存得到的所有后缀及其对应的频数，初始传入空字典
    :param start_node: TrieNode, 查询的起始结点，用于子树的查询
    :return:
    """
    if start_node: # 如果有输入查询起点
        cur_node = start_node # 当前节点就是查询起点
        prefix_node = start_node.parent # 表示查询起点的前一个前缀节点
    else: # 如果没有输入查询起点
        cur_node = self.root # 将当前节点初始化为根节点
        prefix_node = self.root # 表示查询起点的前一个前缀节点，此处也初始化为根节点
    
    mark = True # 标记：从查询起点开始是否成功匹配上了目标序列片段
    
    # 匹配目标序列片段：必须从序列片段的第一个结点开始对比
    for i in range(len(sequence)):
        if i == 0: # 对于目标片段的第一个字符和第一个当前节点
            if sequence[i] != cur_node.value: # 若第一个字符和第一个当前节点就不匹配
                for child_node in cur_node.children.values(): # 则匹配失败，重新对当前节点的所有孩子递归地调用本函数
                    self.search_part(sequence, prefix, suffix, child_node)
                mark = False # 未能从查询起点直接匹配目标序列片段
                break
            else: # 若第一个字符成功匹配上第一个当前节点，则进入下一个循环（进入下一个循环时 i 增大了 1 而 cur_node 没变，因此之后都是当前字符和当前节点的孩子节点进行匹配）
                continue
        else: # i >= 1 的情况下
            if sequence[i] not in cur_node.children: # 若当前节点的所有孩子都不能匹配上序列片段的当前字符
                for child_node in cur_node.children.values(): # 则匹配失败，重新对当前节点的所有孩子递归地调用本函数
                    self.search_part(sequence, prefix, suffix, child_node)
                mark = False # 未能从查询起点直接匹配目标序列片段
                break
            else: # 若当前节点的某个孩子成功匹配上序列片段的当前字符，则将这个孩子节点作为新的当前节点
                cur_node = cur_node.children[sequence[i]]
    
    # 若匹配成功：则字典树的 start_node ~ cur_node 部分完全匹配了目标序列片段
    # 之后进行匹配成功部分的前缀和后缀的提取
    if mark: # 若从查询起点开始成功匹配上了目标序列片段
        if prefix_node.value: # start_node 的父节点就是前缀：若该前缀存在，则进行提取
            if prefix_node.value in prefix:
                prefix[prefix_node.value] += cur_node.count
            else:
                prefix[prefix_node.value] = cur_node.count
        for suffix_node in cur_node.children.values(): # cur_node 的子节点就是后缀
            if suffix_node.value in suffix:
                suffix[suffix_node.value] += suffix_node.count
            else:
                suffix[suffix_node.value] = suffix_node.count
        
        # 已经匹配成功的部分提取结束，但是字典树之后的结构中可能还有其他的位置能够匹配目标字符；
        # 因此对于当前节点的孩子节点继续递归地调用本函数
        for child_node in cur_node.children.values():
            self.search_part(sequence, prefix, suffix, child_node)

2.5. 实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
if __name__ == "__main__":
    trie = Trie()
    texts = [["葬爱", "少年", "葬爱", "少年", "慕周力", "哈哈"], ["葬爱", "少年", "阿西吧"], ["烈", "烈", "风", "中"], ["忘记", "了", "爱"],
             ["埋葬", "了", "爱"]]
    for text in texts:
        trie.insert(text)
    markx = trie.search(["忘记", "了", "爱"])
    print(markx)
    markx = trie.search(["忘记", "了"])
    print(markx)
    markx = trie.search(["忘记", "爱"])
    print(markx)
    markx = trie.delete(["葬爱", "少年", "王周力"])
    print(markx)
    prefixx = {}
    suffixx = {}
    trie.search_part(["葬爱", "少年"], prefixx, suffixx)
    print(prefixx)
    print(suffixx)

输出结果： 

1
2
3
4
5
6
True
False
False
False
{'少年': 1}
{'葬爱': 1, '阿西吧': 1, '慕周力': 1}

3. 完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
# -*- coding:utf-8 -*-
"""
Description:大变双向字典树
迭代次数默认最大999，可以增加但是没必要。其实能深到999层，那这个序列还是选择另外的处理方式吧。

@author: WangLeAi
@date: 2018/8/15
"""

# 定义字典树的节点
class TrieNode(object):
    def __init__(self, value=None, count=0, parent=None):
        # 值：记录此节点对应的字符
        self.value = value
        # 频数统计：统计在插入的所有序列中，此节点被使用到的次数
        self.count = count
        # 父结点：记录此节点的父节点
        self.parent = parent
        # 子节点：记录此节点的所有子节点：以 {value:TrieNode} 的形式
        self.children = {}
        # 终止符号：标记此节点是不是终止节点
        self.isEnd = False

# 定义字典树
class Trie(object):
    def __init__(self):
        # 创建空的根节点
        self.root = TrieNode()

    # 插入操作
    def insert(self, sequence):
        """
        基操，插入一个序列
        :param sequence: list, 需要插入的序列
        :return:
        """
        cur_node = self.root
        for item in sequence:
            if item not in cur_node.children:
                # 插入结点
                child = TrieNode(value=item, count=1, parent=cur_node)
                cur_node.children[item] = child
                # 将插入的节点作为新的当前节点
                cur_node = child
            else:
                # 沿着字典树往下走到对应的子节点
                cur_node = cur_node.children[item]
                cur_node.count += 1
        # 最后标记终止节点
        cur_node.isEnd = True
    
    # 查询操作
    def search(self, sequence):
        """
        基操，查询是否存在完整序列
        :param sequence: list, 需要查询的序列
        :return mask: bool, 表示在字典树中是否查到该序列
        """
        cur_node = self.root
        mark = True # 用于标记是否查询到目标序列
        for item in sequence:
            if item not in cur_node.children:
                mark = False
                break
            else:
                cur_node = cur_node.children[item]
        # 如果目标序列的最后一个节点不是终止节点，则说明目标序列只是字典树中某些序列的前缀部分
        if not cur_node.isEnd:
            mark = False
        return mark

    # 删除操作
    def delete(self, sequence):
        """
        基操，删除序列，准确来说是减少计数
        :param sequence: list, 需要删除的序列
        :return mark: bool, 表示该序列是否在字典树中
        """
        mark = False # 用于标记是否查询到目标序列
        isDeleted = False # 用于标记是否有节点被实际删去
        if self.search(sequence):
            mark = True
            cur_node = self.root
            for item in sequence:
                # 目标序列涉及到的节点的频数计数 -1
                cur_node.children[item].count -= 1
                # 若目标序列涉及到的某个节点的频数计数减少到 0 时，删去该节点；
                # 被删去的节点的所有后代节点都随着该节点一起被直接删去了，因此可以直接 break；
                # 注意：目标序列的最后一个节点肯定也被同时删去了，因此不需要对任何节点的 isEnd 进行操作
                if cur_node.children[item].count == 0:
                    cur_node.children.pop(item)
                    isDeleted = True # 有节点被实际删去了
                    break
                # 否则继续进入下一个节点
                else:
                    cur_node = cur_node.children[item]
            # 如果没有节点被实际删去，说明目标序列只是字典树中某些序列的前缀，删除操作只是将相关节点的频数计数减少了 1
            # 因此，需要将目标序列最后一个节点的 isEnd 值重新设置为 False 表示该序列被删除了
            if not isDeleted:
                cur_node.isEnd = False
        return mark

    # 进阶：查找序列片段在字典树中的所有前缀或后缀
    def search_part(self, sequence, prefix, suffix, start_node=None):
        """
        递归查找子序列，返回前缀和后缀结点
        此处简化操作，仅返回一位前后缀的内容与频数
        :param sequence: list, 输入的序列片段
        :param prefix: dict, {value:count}, 用于保存得到的所有前缀及其对应的频数，初始传入空字典
        :param suffix: dict, {value:count}, 用于保存得到的所有后缀及其对应的频数，初始传入空字典
        :param start_node: TrieNode, 查询的起始结点，用于子树的查询
        :return:
        """
        if start_node: # 如果有输入查询起点
            cur_node = start_node # 当前节点就是查询起点
            prefix_node = start_node.parent # 表示查询起点的前一个前缀节点
        else: # 如果没有输入查询起点
            cur_node = self.root # 将当前节点初始化为根节点
            prefix_node = self.root # 表示查询起点的前一个前缀节点，此处也初始化为根节点
        
        mark = True # 标记：从查询起点开始是否成功匹配上了目标序列片段
        
        # 匹配目标序列片段：必须从序列片段的第一个结点开始对比
        for i in range(len(sequence)):
            if i == 0: # 对于目标片段的第一个字符和第一个当前节点
                if sequence[i] != cur_node.value: # 若第一个字符和第一个当前节点就不匹配
                    for child_node in cur_node.children.values(): # 则匹配失败，重新对当前节点的所有孩子递归地调用本函数
                        self.search_part(sequence, prefix, suffix, child_node)
                    mark = False # 未能从查询起点直接匹配目标序列片段
                    break
                else: # 若第一个字符成功匹配上第一个当前节点，则进入下一个循环（进入下一个循环时 i 增大了 1 而 cur_node 没变，因此之后都是当前字符和当前节点的孩子节点进行匹配）
                    continue
            else: # i >= 1 的情况下
                if sequence[i] not in cur_node.children: # 若当前节点的所有孩子都不能匹配上序列片段的当前字符
                    for child_node in cur_node.children.values(): # 则匹配失败，重新对当前节点的所有孩子递归地调用本函数
                        self.search_part(sequence, prefix, suffix, child_node)
                    mark = False # 未能从查询起点直接匹配目标序列片段
                    break
                else: # 若当前节点的某个孩子成功匹配上序列片段的当前字符，则将这个孩子节点作为新的当前节点
                    cur_node = cur_node.children[sequence[i]]
        
        # 若匹配成功：则字典树的 start_node ~ cur_node 部分完全匹配了目标序列片段
        # 之后进行匹配成功部分的前缀和后缀的提取
        if mark: # 若从查询起点开始成功匹配上了目标序列片段
            if prefix_node.value: # start_node 的父节点就是前缀：若该前缀存在，则进行提取
                if prefix_node.value in prefix:
                    prefix[prefix_node.value] += cur_node.count
                else:
                    prefix[prefix_node.value] = cur_node.count
            for suffix_node in cur_node.children.values(): # cur_node 的子节点就是后缀
                if suffix_node.value in suffix:
                    suffix[suffix_node.value] += suffix_node.count
                else:
                    suffix[suffix_node.value] = suffix_node.count
            
            # 已经匹配成功的部分提取结束，但是字典树之后的结构中可能还有其他的位置能够匹配目标字符；
            # 因此对于当前节点的孩子节点继续递归地调用本函数
            for child_node in cur_node.children.values():
                self.search_part(sequence, prefix, suffix, child_node)


if __name__ == "__main__":
    trie = Trie()
    texts = [["葬爱", "少年", "葬爱", "少年", "慕周力", "哈哈"], ["葬爱", "少年", "阿西吧"], ["烈", "烈", "风", "中"], ["忘记", "了", "爱"],
             ["埋葬", "了", "爱"]]
    for text in texts:
        trie.insert(text)
    markx = trie.search(["忘记", "了", "爱"])
    print(markx)
    markx = trie.search(["忘记", "了"])
    print(markx)
    markx = trie.search(["忘记", "爱"])
    print(markx)
    markx = trie.delete(["葬爱", "少年", "王周力"])
    print(markx)
    prefixx = {}
    suffixx = {}
    trie.search_part(["葬爱", "少年"], prefixx, suffixx)
    print(prefixx)
    print(suffixx)

Author：Lingfeng Zhu

Original Link：https://lingfengzhu.github.io/2021/01/06/Trie-Tree/

Published：January 6th 2021, 8:39:12 pm

Updated：December 28th 2021, 11:35:17 am

Copyright：This Article Uses Attribution-NonCommercial 4.0 International as the license

CATALOG
  1. 1. 基本介绍
    1. 1.1. 定义
    2. 1.4. 优缺点
  2. 2. 代码实现
    1. 2.1. 插入操作：将一个序列插入字典树
    2. 2.2. 查找操作：查询一个序列是否在字典树中
    3. 2.3. 删除操作：从字典树中删去一个序列
    4. 2.4. 进阶：查找序列片段在字典树中的所有前缀或后缀
    5. 2.5. 实例
  3. 3. 完整代码
Total : 33
2022
2021
2020
NLP Survival Analysis COVID-19 Conda Docker Python Hexo Web-Frontend Pytorch RecSys
Deep-Learning Algorithm Statistics Syntax Machine-Learning Finance